Workshop - Erweitertes Clustering
 Folie - Daten mit OpenRefine clustern
Folie - Daten mit OpenRefine clusternWir verwenden eigene Clustering Methoden in OpenRefine, um Schreibweisen zu vereinheitlichen.
Clustering in der OpenRefine Dokumentation.
Clustering im OpenRefine Wiki.
Einsteiger Workshop 05 Daten mit OpenRefine clustern.
Dieser Workshop wurde zuletzt getestet mit OpenRefine Version 3.9.3.
Daten
Wir benötigen die folgenden Dateien als OpenRefine Projekt:
Erweitertes Clustering💾 Wir benötigen die folgende Datei (Rechtsklick und “Ziel speichern unter…”):
In der nachfolgenden Tabelle sind typische Probleme dargestellt, die mit den Standard Clusteringverfahren von OpenRefine nicht direkt zu lösen sind.
| Ort | Name | Name 2 |
|---|---|---|
| XY, Ort in Bayern | Hans Meier | Hans Meier |
| XY (Bayern) | Maier, Hans | Hans Peter Meier |
| XY in Bayern | Hans Peter Meyer | Hans P. Meier |
| XY; Bayern | Hans (Peter) Maier | Hans (Peter) Meier |
| XY | Bayern | Hans P. Mayer | Hans Müller |
| XY, liegt in Bayern | Meier, Hans (Peter) | Hans Peter Müller |
In der Spalte Ort gibt es unterschiedliche Ansetzungen für einen Ort in Bayern. Die Spalte Name enthält unterschiedliche Schreibweisen für den Namen Hans Peter Meier. Und die Spalte Name 2 enthält Hans Peter Meier und Hans Peter Müller jeweils mit und ohne Zweitnamen.
Keying Functions
Eine von OpenRefine unterstützte Art des Clusterings sind so genannte key collision Verfahren.
Die Idee dahinter ist, dass ein Eingabetext nach einheitlichen Regeln umgewandelt wird. Die Ergebnisse der Umwandlungen werden dann verglichen und die gleichen Ergebnisse zusammengefasst.
Typische Beispiele für Umwandlungsregein sind:
- Wörter sortieren
- Sonderzeichen entfernen oder umwandeln
- Wörter auf Normalformen bringen
- Synonyme auflösen
- n-Gramme erstellen
- …
Einige dieser Methoden sind in OpenRefine implementiert. Dennoch sind sie häufig nicht ausreichend für spezifischere Probleme. Seit OpenRefine 3.9.3 ist es möglich eigene Clustering Algorithmen in den von OpenRefine unterstützten Programmiersprachen zu hinterlegen.
Im Folgenden stellen werden zwei Algorithmen für das Keying vorstellt.
OrtFingerprint
Das Problem bei den Werten in der Spalte Ort ist, dass wir unterschiedliche Sonderzeichen, als auch “überflüssige” Wörter haben, die eine Zusammenführung via Clustering erschweren.
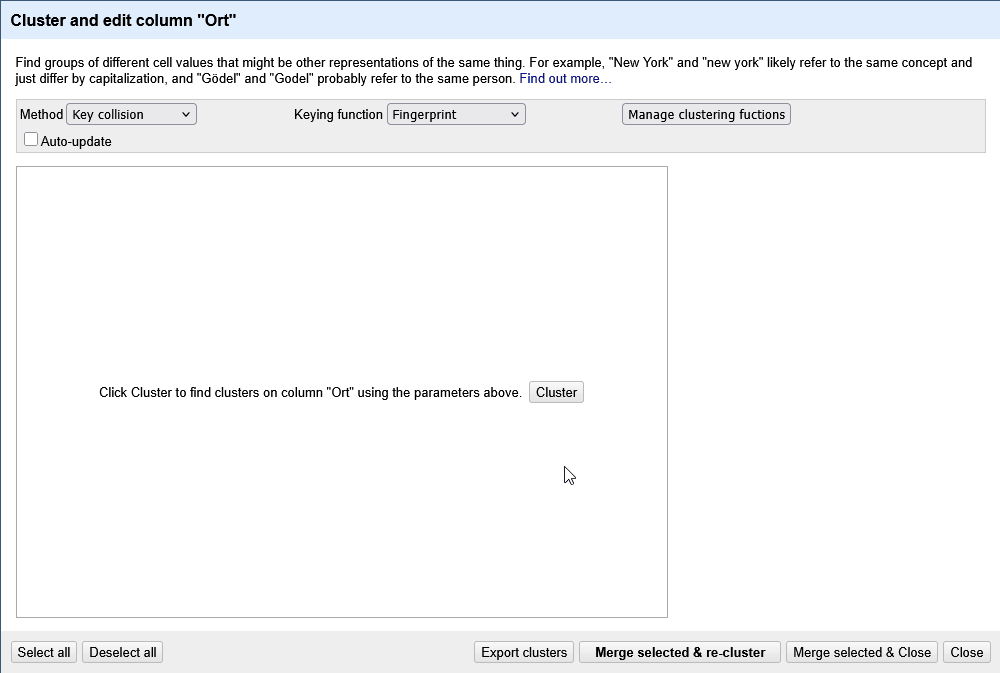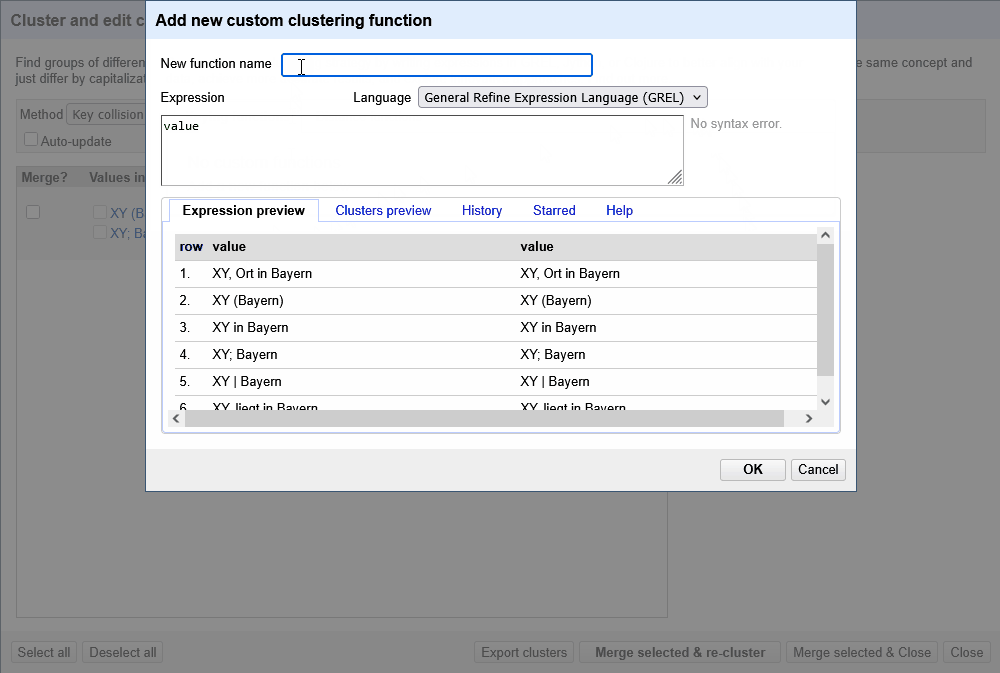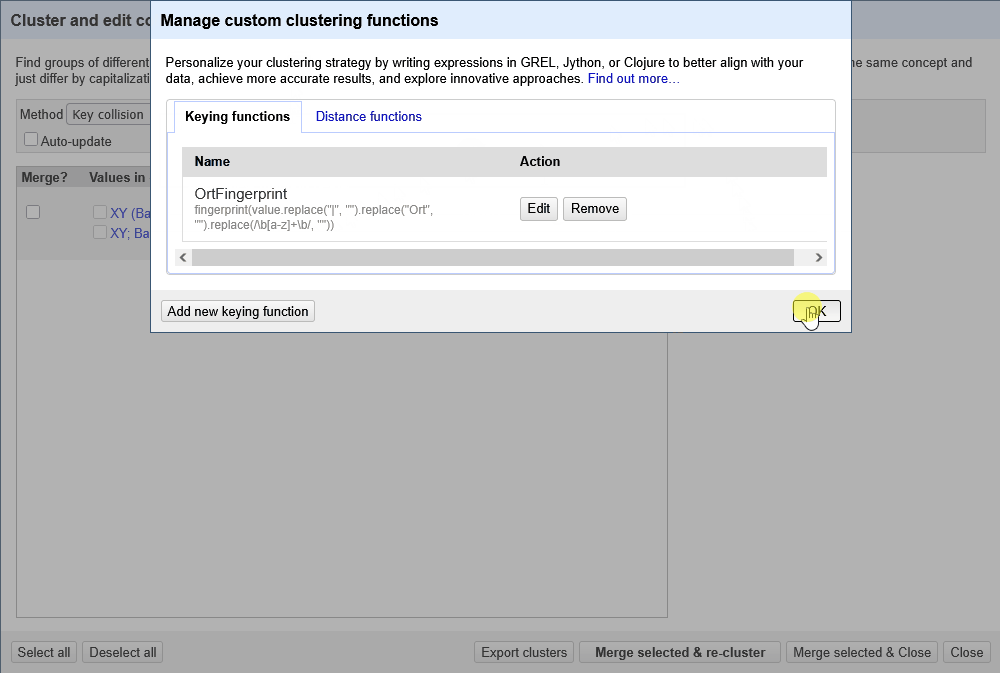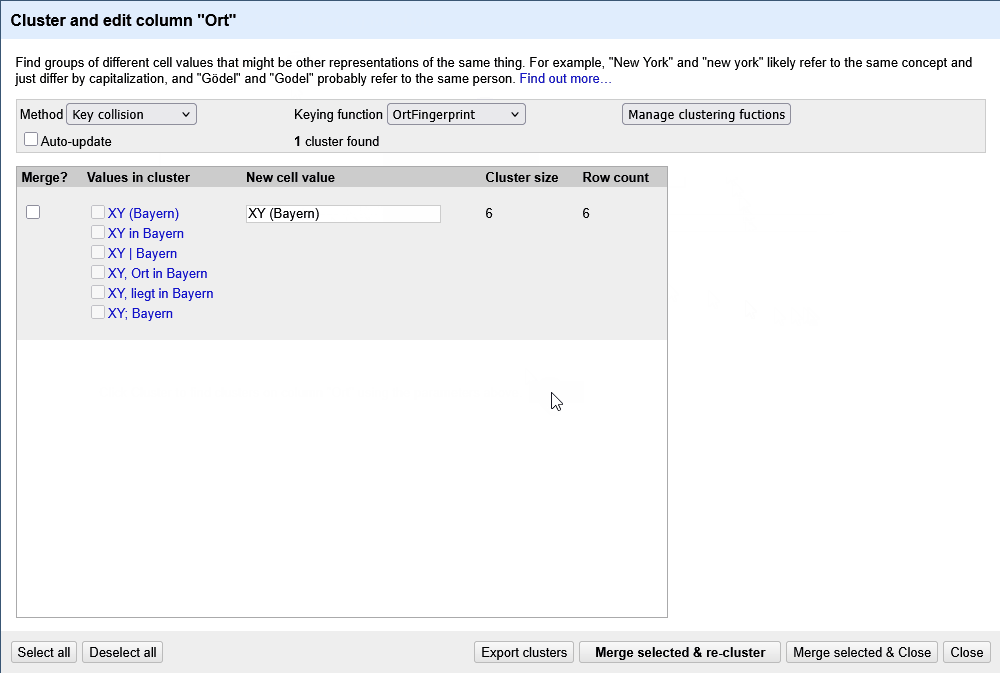
Der Screencast in Abbildung 1 zeigt, wie im Clustering Dialog unter Manage clustering functions eigene Clustering Funktionen hinterlegt werden. In dem Beispiel ist das ein GREL-Ausdruck, der die Fingerprint Methode von OpenRefine mit unserem domänenspezifischem Wissen kombiniert.
In dem nachfolgenden GREL-Ausdruck werden vor der Anwendung der Fingerprint Methode von Openrefine die folgenden Schritte durchgeführt:
- Sonderzeichen entfernen, die die Fingerprint Methode nicht berücksichtigt (
"|"). - Stoppworte entfernen (
"Ort"). - Klein geschriebene Wörter entfernen (
/\b[a-z]+\b/).
fingerprint(value.replace("|", "").replace("Ort", "").replace(/\b[a-z]+\b/, ""))
Das Ergebnis ist eine spezifische Fingerprintmethode, die wie in Abbildung 1 gezeigt, unterschiedliche Ansetzungen bei Orten berücksichtigen kann.
CologneFingerprint
Die in OpenRefine implementierten Clustering-Methoden lassen sich nachnutzen und kombinieren. Der folgende GREL-Ausdruck wendet zuerst das Fingerprinting und dann die Normalisierung bzgl. der deutschen Aussprache mit Cologne Phonetic an.
fingerprint(value).phonetic("cologne-phonetic")
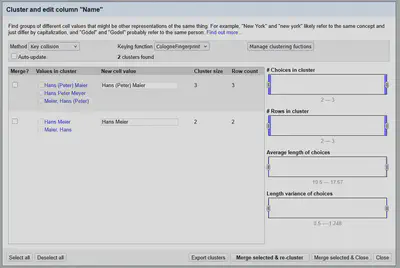
Auf diese Weise können die Werte in der Spalte Name wie in Abbildung 2 gezeigt (größtenteils) zusammengeführt werden.
Distance Functions
Bei den Distanzfunktionen werden die Texte nicht umgewandelt, sondern mit unterschiedlichen Metriken berechnet, wie “weit” sie voneinander entfernt sind. Dafür erhält man Zugriff auf die Variablen value1 und value2 und gibt eine Zahl zurück, die die Distanz zwischen den beiden Werten repräsentiert. Je größer die Zahl, desto “unähnlicher” sind die Texte.
Manche Algorithmen betrachten auch positiv die Ähnlichkeit (Similarity) von Texten. Dabei sind die beiden Metriken einfach umzurechnen: $distance = 1 - similarity$.
Manche Algorithmen betrachten die Ähnlichkeit bzw. die Distanz auch nicht als Wert zwischen 0 und 1.0, sondern zwischen 0 und 100.
FingerprintDistance
Ein typisches Problem ist, dass man sowohl unterschiedliche Ansetzungen, als auch leichte Abweichungen hat. Hier lässt sich zum Beispiel das Fingerprinting in OpenRefine mit der Implementierung der Levenshtein-Distanz kombinieren.
levenshteinDistance(fingerprint(value1), fingerprint(value2))
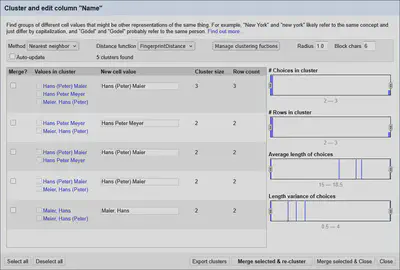
In Abbildung 3 sind die Ergebnisse der kombinierten Algorithmen auf der Spalte Name gezeigt.
AbsoluteDistance
In der Spalte Name 2 ist das Problem mit Extrabegriffen wie Zweitnamen etwas deutlicher gezeigt. Hier könnte man Methoden anwenden, die Distanzen auf Wortebene berechnen.
Im Folgenden Code Beispiel ist ein Jython-Algorithmus, der die Datenstruktur Counter verwendet um eine Art Bag-of-words Model zu erstellen.
Die Distanz ist hier, die Anzahl an unterschiedlichen Worten zwischen den beiden Texten.
import re
from collections import Counter
splitter = re.compile(r"\W+")
words = Counter(splitter.split(value1.strip()))
words.subtract(Counter(splitter.split(value2.strip())))
dist = sum(abs(count) for count in words.values())
return dist
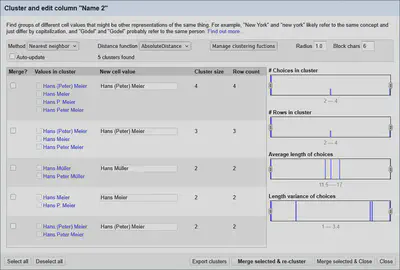
Wie in Abbildung 4 gezeigt, hilft diese Methode bei dem Problem von einzelnen Extrabegriffen, die den auf Buchstabenebene arbeitenden Levenshtein-Algorithmus “überfordern”.
CosineDistance
Eine wichtige Distanzmetrik zur Berechnung der Ähnlichkeit (oder in dem Fall der Distanz) zwischen Vektoren ist die Kosinus-Ähnlichkeit. Dies ist exemplarisch in dem folgenden Jython-Code umgesetzt.
import re
from collections import Counter
splitter = re.compile(r"\W+")
a = Counter(splitter.split(value1.strip()))
b = Counter(splitter.split(value2.strip()))
words = list(set(a) | set(b))
a_vec = [a.get(word, 0) for word in words]
b_vec = [b.get(word, 0) for word in words]
v_len = lambda v: sum(x * x for x in v) ** 0.5
v_dot = lambda v1, v2: sum(x * y for x, y in zip(v1, v2))
dist = 1 - v_dot(a_vec, b_vec) / (v_len(a_vec) * v_len(b_vec))
return dist
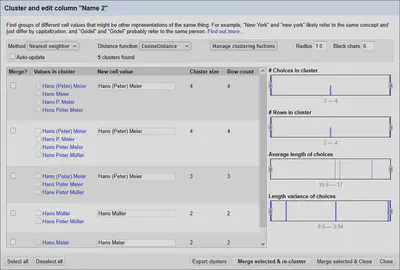
Ähnlich wie bei der AbsoluteDistance zählen wir, wie oft ein Wort im Text vorkommt. Diesmal berücksichtigen wir (vereinfacht ausgedrückt) zusätzlich die Länge der Texte. Dadurch ist der Rückgabewert eine Zahl zwischen 0 und 1. Wie in Abbildung 5 gezeigt, erhält man mit dem in OpenRefine voreingestellten Standardradius von 1.0 dadurch alle möglichen Cluster. Für sinnvolle Ergebnisse sollte man den Radius bei Verwendung der Kosinus-Ähnlichkeit also auf Werte zwischen 0.1 und 0.3 reduzieren.
Weitere Ideen
Mit Jython lassen sich auch Skripte auf dem eigenen Rechner ausführen oder Web-APIs ansprechen. Damit kann man komplexere und effizientere Algorithmen implementieren und/oder auf andere Python Pakete zurückgreifen.
Hier ist eine kleine Sammlung von weiteren Ideen:
- Keying
- Liste mit Synonymen einlesen und Synonym-Cluster-ID zurückgeben.
- Lemma, Normalform oder Lexem berechnen z.B. mit spaCy.
- …
- Distance
Fazit
Eigene Clustering-Funktionen hinterlegen zu können ermöglicht komplett andere Arbeitsabläufe und reduziert regelmäßige manuelle Nacharbeiten.
In Kombination mit der Möglichkeit z.B. über Jython Web-APIs anzusprechen, können zusätzlich Funktionalitäten von externen Werkzeugen für das Clustering genutzt werden.
Im nächsten Teil beschäftigen wir uns Python mit OpenRefine zu verwenden.